前几天读了《复杂》。对复杂学的研究,在人工智能重获热度的今天,似乎获得了新的意义——当然,我们还是不知道炼金术的大锅里面发生了什么。
幂律分布/Zipf定律/帕累托法则/80-20定律/whatever,本质上是同一种东西。这种分布模式和正态分布类似,广泛存在于大自然和人造物的各个角落。一般来说,对于具有:
- 优先连接性(Preferential attachment)/马太效应
- “凡有的,还要加给他,叫他有余;没有的,连他所有的也要夺过来。”
- 成长性
- 网络的尺度不受客观条件的限制,可以无限增长
的网络,其节点连接数较为满足幂律分布。
Youtube上有个视频对幂律分布讲得很清楚,对其中提到的两个实验,我利用python进行了模拟。模拟中使用的jupyter notebook文件放在了github gist上。
猴子和打字机
一只猴子(我们叫它Shashi Biya)在打字机上乱敲,它敲二十六个字母和空格概率都相等。那么,咱们能不能看出他的用词习惯?答案是肯定的。
import string,random
from collections import Counter
s=string.ascii_lowercase+" "
s="abcd "
monkey=''.join(random.choices(s, k=10000000))
monkey=[m for m in monkey.split(" ") if m]
c=Counter(monkey)
common=c.most_common()[:10000]
fre=[value for (key,value) in common]
plt.plot(fre)
plt.xscale('log')
plt.yscale('log')
plt.show()
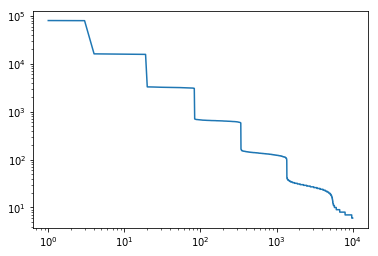
阶梯形状可能是由于概率相等
我们的这位大文豪颇有古风,喜欢用单字(“a”)胜过长单词(“ffsda”),而且用词比例正符合幂律分布:在双log坐标系下,图像大致是一条直线。这很符合直觉:为了得到任何长度大于1的单词,猴子第二次敲的按钮必须不是空格。
不要嘲笑我们的前辈,人类的语言也具有相同的性质,虽然概率最高的字是the什么的。并不是Zipf’s law限制了猴子打出十四行诗,这或许是个好消息。
连接曲别针,第一种方法
在墙上钉100个钉子,然后随意把曲别针连在上面。哪个钉子上曲别针越多,下一个曲别针挂在上面的概率就越高。
l=100
list=np.ones(l)
for i in range(100000):
s=sum(list)
p=[j/s for j in list]
k=np.random.choice(l,1, p=p)
list[k]+=1
plt.plot(sorted(list,reverse=True))
plt.xscale('log')
plt.yscale('log')
plt.show() #指数分布
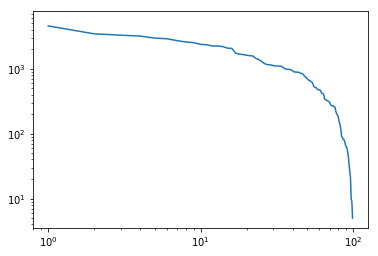
可惜这只是个指数分布
与幂律分布相比,指数分布更加“平缓”,而且在双对数坐标系下也并不是一条直线。
连接曲别针,the right way
现在,我有一把曲别针。我随便拿出两个曲别针,并把它们两个所在的串连接起来。
假设我对每一个曲别针没有特别的爱好,那么,某个串选中的概率,与串中的曲别针个数正相关。这就是所谓的优先连接性。
tic=timeit.default_timer()
l=20000
list=[1]*l
while len(list)>14000:
s=sum(list)
p=[j/s for j in list]
k1=np.random.choice(len(list),1, p=p)
a1=list.pop(k1[0])
s=sum(list)
p=[j/s for j in list]
k2=np.random.choice(len(list),1, p=p)
a2=list.pop(k2[0])
list.append(a1+a2)
toc=timeit.default_timer()
print(toc-tic)
plt.plot(sorted(list,reverse=True))
plt.xscale('log')
plt.yscale('log')
plt.show()
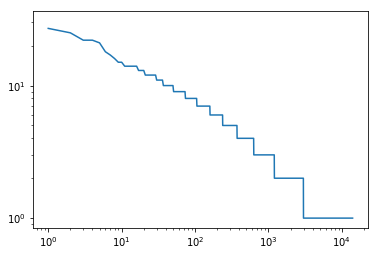
好的,我们得到了 基于曲别针的互联网系统 ——至少可以算是个物联网。在这个网络里,(大概)80%的曲别针在20%的链子中,余下的曲别针散落在另外的地方。我们叫那些链子“曲别针巨头”。随着连接次数越来越多,链子越来越长,分散的曲别针越来越少,这就是“链子中心化”,我们现在互联网的状态。
当继续这个过程的时候,最终(很快)就只剩下唯一一条长链,这就是我们互联网的末日1。
刘慈欣在还没有现在这么出名的时候,写过一篇叫做《赡养人类》的作品,提到了有关“终产者”的概念。当时,有人评论大刘“不懂政治,也不懂经济”,我十分希望这个人是对的。
2018年4年3日的编辑:
这里有另一个Zipf's Law的例子,可以看出,其仍然满足马太效应的性质。另外,别人的故事编的还是好啊。
这似乎和Net neutrality并不是一回事。并没有什么邪恶组织,邪恶的只有系统而已。 ↩︎